Rumus Web mengumpulkan materi Peluang, Permutasi & Kombinasi
Matematika ini untuk anak SMA demi UAN SNMPTN SPMB SIMAK UI. Silakan
dipelajari

 1) Permutasi
1) Permutasi
Permutasi adalah susunan unsur-unsur yang berbeda dalam urutan tertentu. Pada permutasi urutan diperhatikan sehingga

Permutasi k unsur dari n unsur

adalah
semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n
unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis

atau

.
Permutasi siklis (melingkar) dari n unsur adalah (n-1) !
Cara cepat mengerjakan soal permutasi
dengan penulisan nPk, hitung 10P4
kita langsung tulis 4 angka dari 10 mundur, yaitu 10.9.8.7
jadi 10P4 = 10x9x8x7 berapa itu? hitung sendiri 
Contoh permutasi siklis :
Suatu keluarga yang terdiri atas 6 orang duduk
mengelilingi sebuah meja makan yang berbentuk lingkaran. Berapa banyak
cara agar mereka dapat duduk mengelilingi meja makan dengan cara yang
berbeda?
Jawab :
Banyaknya cara agar 6 orang dapat duduk mengelilingi meja makan dengan
urutan yang berbeda sama dengan banyak permutasi siklis (melingkar) 6
unsur yaitu :

2) Kombinasi
Kombinasi adalah susunan unsur-unsur dengan tidak memperhatikan
urutannya. Pada kombinasi AB = BA. Dari suatu himpunan dengan n unsur
dapat disusun himpunan bagiannya dengan untuk

Setiap himpunan bagian dengan k unsur dari himpunan dengan unsur n disebut kombinasi k unsur dari n yang dilambangkan dengan ,

Contoh :
Diketahui himpunan
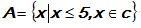
.
Tentukan banyak himpunan bagian dari himpunan A yang memiliki 2 unsur!
Jawab :

Banyak himpunan bagian dari A yang memiliki 2 unsur adalah C (6, 2).
 Cara cepat mengerjakan soal kombinasi
Cara cepat mengerjakan soal kombinasi
dengan penulisan nCk, hitung 10C4
kita langsung tulis 4 angka dari 10 mundur lalu dibagi 4!, yaitu 10.9.8.7 dibagi 4.3.2.1
jadi 10C4 = 10x9x8x7 / 4x3x2x1 berapa itu? hitung sendiri

Ohya jika ditanya 10C6 maka sama dengan 10C4, ingat 10C6=10C4. contoh lainnya
20C5=20C15
3C2=3C1
100C97=100C3
melihat polanya? hehe semoga bermanfaat!
Peluang Matematika
1. Pengertian Ruang Sampel dan Kejadian
Himpunan S dari semua kejadian atau peristiwa yang mungkin mucul dari
suatu percobaan disebut ruang sampel. Kejadian khusus atau suatu unsur
dari S disebut titik sampel atau sampel. Suatu kejadian A adalah suatu
himpunan bagian dari ruang sampel S.
Contoh:
Diberikan percobaan pelemparan 3 mata uang logam sekaligus 1 kali, yang
masing-masing memiliki sisi angka ( A ) dan gambar ( G ). Jika P adalah
kejadian muncul dua angka, tentukan S, P (kejadian)!
Jawab :
S = { AAA, AAG, AGA, GAA, GAG, AGG, GGA, GGG}
P = {AAG, AGA, GAA}
2. Pengertian Peluang Suatu Kejadian
Pada suatu percobaan terdapat n hasil yang mungkin dan masing-masing
berkesempatan sama untuk muncul. Jika dari hasil percobaan ini terdapat k
hasil yang merupakan kejadian A, maka peluang kejadian A ditulis P ( A )
ditentukan dengan rumus :

Contoh :
Pada percobaan pelemparan sebuah dadu, tentukanlah peluang percobaan kejadian muncul bilangan genap!
Jawab : S = { 1, 2, 3, 4, 5, 6} maka n ( S ) = 6
Misalkan A adalah kejadian muncul bilangan genap, maka:
A = {2, 4, 6} dan n ( A ) = 3

3. Kisaran Nilai Peluang Matematika
Misalkan A adalah sebarang kejadian pada ruang sampel S dengan n ( S ) = n, n ( A ) = k dan

Jadi, peluang suatu kejadian terletak pada interval tertutup [0,1].
Suatu kejadian yang peluangnya nol dinamakan kejadian mustahil dan
kejadian yang peluangnya 1 dinamakan kejadian pasti.
4. Frekuensi Harapan Suatu Kejadian
Jika A adalah suatu kejadian pada frekuensi ruang sampel S dengan
peluang P ( A ), maka frekuensi harapan kejadian A dari n kali percobaan
adalah n x P( A ).
Contoh :
Bila sebuah dadu dilempar 720 kali, berapakah frekuensi harapan dari munculnya mata dadu 1? Jawab :
Pada pelemparan dadu 1 kali, S = { 1, 2, 3, 4, 5, 6 } maka n (S) = 6.
Misalkan A adalah kejadian munculnya mata dadu 1, maka:
A = { 1 } dan n ( A ) sehingga : 
Frekuensi harapan munculnya mata dadu 1 adalah

5. Peluang Komplemen Suatu Kejadian
Misalkan S adalah ruang sampel dengan n ( S ) = n, A adalah kejadian
pada ruang sampel S, dengan n ( A ) = k dan Ac adalah komplemen kejadian
A, maka nilai n (Ac) = n – k, sehingga :

Jadi, jika peluang hasil dari suatu percobaan adalah P, maka peluang hasil itu tidak terjadi adalah (1 – P).
Peluang Kejadian Majemuk
1. Gabungan Dua Kejadian
Untuk setiap kejadian A dan B berlaku :

Catatan :

dibaca “ Kejadian A atau B dan

dibaca “Kejadian A dan B”
Contoh :
Pada pelemparan sebuah dadu, A adalah kejadian munculnya bilangan
komposit dan B adalah kejadian muncul bilangan genap. Carilah peluang
kejadian A atau B!
Jawab :

2. Kejadian-kejadian Saling Lepas
Untuk setiap kejadian berlaku

Jika

. Sehingga

Dalam kasus ini, A dan B disebut dua kejadian saling lepas.
3. Kejadian Bersyarat
Jika P (B) adalah peluang kejadian B, maka P (A|B) didefinisikan sebagai peluang kejadian A dengan syarat B telah terjadi. Jika

adalah peluang terjadinya A dan B, maka

Dalam kasus ini, dua kejadian tersebut tidak saling bebas.
4. Teorema Bayes
Teorema Bayes(1720 – 1763) mengemukakan hubungan antara P (A|B) dengan P ( B|A ) dalam teorema berikut ini :
 5. Kejadian saling bebas Stokhastik
5. Kejadian saling bebas Stokhastik
(i) Misalkan A dan B adalah kejadian – kejadian pada ruang sampel S, A
dan B disebut dua kejadian saling bebas stokhastik apabila kemunculan
salah satu tidak dipengaruhi kemunculan yang lainnya atau : P (A | B) = P
(A), sehingga:

Sebaran Peluang
1. Pengertian Peubah acak dan Sebaran Peluang.
Peubah acak X adalah fungsi dari suatu sampel S ke bilangan real R. Jika
X adalah peubah acak pada ruang sampel S denga X (S) merupakan himpunan
berhingga, peubah acak X dinamakan peubah acak diskrit. Jika Y adalah
peubah acak pada ruang sampel S dengan Y(S) merupakan interval, peubah
acak Y disebut peubah acak kontinu. Jika X adalah fungsi dari sampel S
ke himpunan bilangan real R, untuk setiap

dan setiap

maka:

Misalkan X adalah peubah acak diskrit pada ruang sampel S, fungsi
masa peluang disingkat sebaran peluang dari X adalah fungsi f dari R
yang ditentukan dengan rumus berikut :
 2. Sebaran Binom
2. Sebaran Binom
Sebaran Binom atau Distribusi Binomial dinyatakan dengan rumus sebagai berikut :

Dengan P sebagai parameter dan

Rumus ini dinyatakan sebagai:

untuk n = 0, 1, 2, …. ,n
Dengan P sebagai parameter dan

P = Peluang sukses
n = Banyak percobaan
x = Muncul sukses
n-x = Muncul gagal
Rumus Peluang


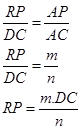

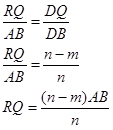

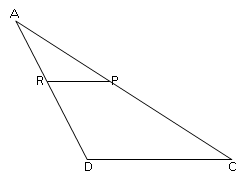
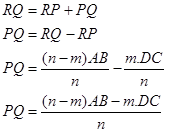
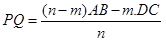


 adalah
semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n
unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis
adalah
semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n
unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis  atau
atau  .
.

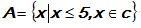 .
.








 dibaca “ Kejadian A atau B dan
dibaca “ Kejadian A atau B dan  dibaca “Kejadian A dan B”
dibaca “Kejadian A dan B”
 Jika
Jika  . Sehingga
. Sehingga  Dalam kasus ini, A dan B disebut dua kejadian saling lepas.
Dalam kasus ini, A dan B disebut dua kejadian saling lepas. Dalam kasus ini, dua kejadian tersebut tidak saling bebas.
Dalam kasus ini, dua kejadian tersebut tidak saling bebas.

 dan setiap
dan setiap  maka:
maka:



 untuk n = 0, 1, 2, …. ,n
untuk n = 0, 1, 2, …. ,n